When we represent the equation of a line, the concept of the slope-intercept form of the straight line is used. If coordinates of any straight line equation are given slope-intercept form is used in this case. The reason is that this equation is called the straight line equation because they satisfy all point passing through the line.
The slope-intercept form provides a clear and concise way to express linear equations, making it an essential tool in algebra and mathematics in general. The slope-intercept form is exceptionally useful for various applications, including graphing linear equations, understanding linear relationships, and making predictions.
In this article, we will discuss the definition of slope intercept form, formula derivation, and converting standard form into slope form. Moreover, with the help of practical examples, a topic is more explained for better understanding.
What is slope intercept form?
A straight line of the slope-intercept form is used to find the equation of the line. And for the formula of slope intercept form, we know the equation of line called y-intercept on the b point and m is the slope. The formula of slope intercept form is denoted given below.
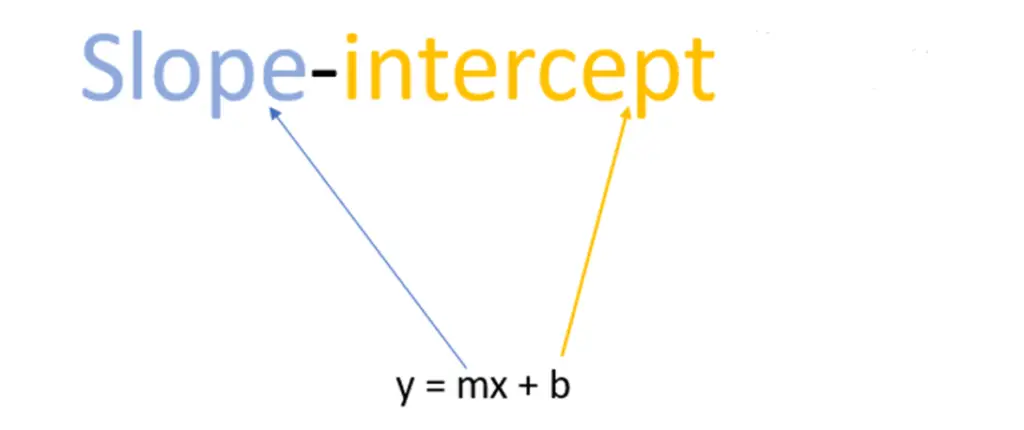
Derivation of Formula of slope intercept form
The formula for the slope-intercept form of a linear equation, y = mx + b, can be derived from basic principles in algebra and geometry. We follow these steps by finding the derivation of the slope.
Step 1: Understand the Slope (m)
The slope of the line is defined as the change in the vertical (y) coordinate divided by the change in the horizontal (x) coordinate between two points on the line. Mathematically, the slope (m) is calculated as:
m = Change in y/change in x
Step 2: Calculate the Slope between Two Points
The slope m between these two points is:
m= y2 – y1/ x2 – x1
Step 3: equation determine
Now, at every point on the line, we wish to identify an equation that connects (x) and (y). This equation should also include the slope (m).
Start with the point-slope form of a linear equation, which relates a point (x1, y1) and the slope (m):
y – y1 = m (x – x1)
Step 4: Solve for (y)
To get the equation in slope-intercept form, we’ll isolate \(y\) on the left side:
y = y1 + m (x – x1)
Step 5: Use a Specific Point
We can rewrite it as just (b) to simplify:
y = b + m (x – x1)
Step 6: Final Form
Now, our equation relates (x) and (y) with the slope (m) and a constant (b):
y = mx + b
In addition, there you have it, the formula for the slope-intercept form of a linear equation, y = mx + b, where m represents the slope, and (b) represents the y-intercept. This form is incredibly useful for graphing lines and understanding linear relationships in algebra.
Conversion of Standard form equation into slope intercept form
Converting a linear equation from standard form to slope-intercept form (y = mx + b) involves rearranging the equation to solve for y while isolating it on one side of the equation.
Consider the linear equation Ax + By = C
In this equation (A) is typically positive (A), (B), and (C) are constants. (y) and (x) are variables corresponding to line-point coordinates.
- Converting to Slope-Intercept Form (y = mx + b):
Isolate the y term on one side of the equation: Subtract (Ax) from both sides of the equation to move the (Ax) term to the right-hand side. After that, we get -Ax + C.
- B divide
Y is the coefficient divided by both sides with them (which is (B) to isolate (y).
y = (-Ax + C)/B
- Rearrange for clarity:
You can rearrange the right side of the equation to make it more readable. This step isn’t required, but it can help you see the slope (m) and y-intercept (b) more clearly.
y = (-A/B) x +C/B
Now, you have the equation in slope-intercept form (y = mx + b) where:
The slope of the line = -A/B
b = C/B is the y-intercept, representing the point where the line crosses the y-axis.
How to determine straight-line equation?
Example 1:
Consider the value of two points of slope is given (x1, y1) = (6, 5) and (x2, y2) = (10, 9).
The slope of a line?
Solution:
Straight-line equation is
y = mx + b (1)
Step 1: find the slope
m = (y2-y1)/(x1-x2)
m = (9) – (5)/ (10) – (6)
m = (4)/4
m = 1
Now putting the value of m in equation (1)
y = 1x + b (2)
Step 2: determine the b.
Let’s choose the first point, (10, 9) for calculating the y-intercept:
y = mx + b
9 = 1(10) + b
9 = 10 + b
9 – 10 = b
b = -1
Now putting the value of b in equation (2)
y = 1x + (-1)
y = 1x – 1
You can also try a slope intercept equation calculator in order to find the straight line equation through slope intercept form with steps in a couple of seconds.

Solved through slope intercept form calculator by AllMath
Example 2:
If the y-intercept is 5 and the slope is 9 is given find Evaluate the equation straight line.
Solution:
Step 1:
Determine the given data
b= 5
and
m= 9
Step 2:
The formula for the equation of the straight line is:
y= mx + b
Step 3:
Put the required value in the formula
y= 9x+5
Summary
In this article, we have discussed the definition of slope intercept form, formula derivation, and converting standard form into slope form. Moreover, with the help of practical examples, a topic is more explained for better understanding.
FAQs
Q # 1:
What does m in the slope-intercept form stand for?
Answer:
m in the slope-intercept form represents the slope of the line. It indicates the steepness or incline of the line and tells you how much ‘y’ changes for a given change in ‘x’. A positive ‘m’ means the line slopes upward to the right, while a negative ‘m’ means it slopes downward.
Q # 2:
How can I use the slope-intercept form to graph a line?
Answer:
Plotting the y-intercept (the location of (0, b)) is the first step in creating a slope-intercept form graph of a line. Then, if slope ‘m’ is positive or negative, go one unit to the right and up to get the following point.
Q # 3:
Can a slope-intercept form be used to represent any linear equation?
Answer:
Yes, any linear equation can be rearranged into the slope-intercept form y = mx + b, provided that the equation is indeed linear (a straight line). This form is a convenient way to express and understand linear relationships.
Table of Contents
